Table of Contents
Managing uncertainty with Certainty Factors Algebra
This tutorial focuses on the practical aspect of using he CF algebra to model uncertainty in XTT2 models. The detailed information on the theory that stays behind the uncertainty handling mechanism in HeaRTDroid, can be found in Bobek S., Nalepa G. (2016). Uncertainty handling in rule-based mobile context-aware systems, Pervasive and Mobile Computing.
This tutorial is an continuation of the following tutorials:
If you did not read them, please go through them quickly to get a glimpse on the context of the use case.
Use case
In Time-based operators tutorial we added time-parametrized operators to our urban helper application, to decide weather the car was just parked, or has been parked earlier, or maybe has just started.
The user activity that we can obtain from the activity recognition sensor allows us only to recognize the case when the user is in_vehicle.
However, in_vehicle could mean: in a car, in a taxi, in a bus, etc.
Furthermore, the data that comes from the sensor is inherently uncertain – alongside with every reading we get an information about its confidence, which hardly is 100%.
Therefore, we need to have a tool that will allow us to model and potentially decrease somehow this kind of uncertainty. This is where the Certainty Factors algebra come in handy. If you are not familiar with the CF algebra, see Certainty Factors Axioms section.
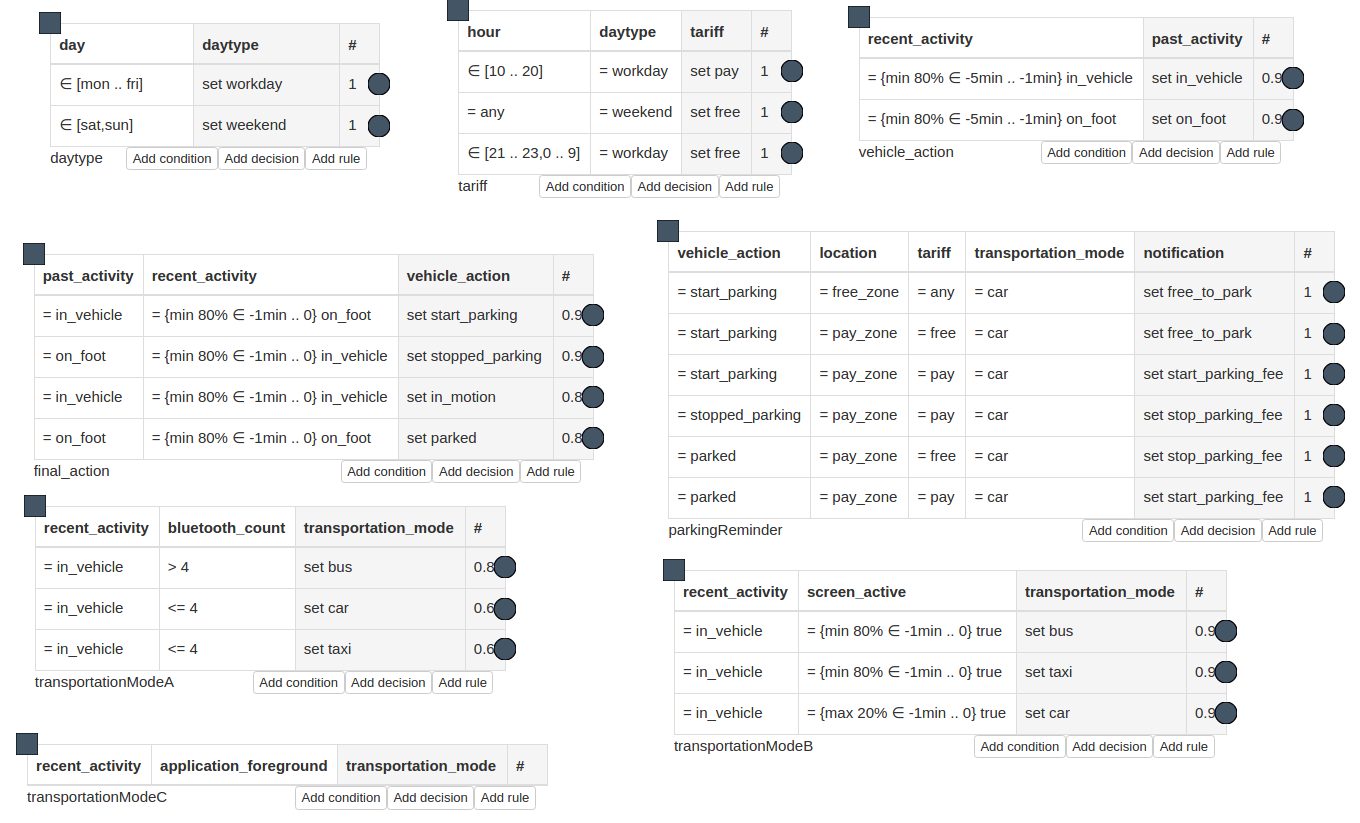
The model that (partially) solves the problem given above is presented in the following figure. The complete model with test scripts and basic callbacks can be downloaded from here.
To run the example, you will need the latest version of HaQuNa:
javac -cp haquna.jar:. *.java java -cp haquna.jar:. haquna.HaqunaMain --console test-script-cf.hqn
The certainty factors (CF) in XTT2 models can be assigned to three different elements:
- to the attributes' values – this is usually done when the value is obtained from context-provier (sensor, user, etc.). This represents the confidence the value is correct.
- to rules conditions – this is evaluated based on the CF of the attribute's value from the condition. The complete set of rules for how to evaluate the CF of conditional formula is given in: Bobek S., Nalepa G. (2016). Uncertainty handling in rule-based mobile context-aware systems, Pervasive and Mobile Computing
- to the rules directly – this assignment is done by the knowledge engineer or machine learning methods. It represents the confidence of the rule itself being correct.
You can see, that for instance table transportationModeA has rules which CF are lower than 1.
It means that the rules themselves are not completely certain and the resulting confidence of the conclusion they produce is not certain as well.
Its certainty is calculated as a product of a minimal CF of the conditions and the confidence of the rule.
For example if the value of recent_activity was in_vehicle, but the confidence of this activity was 0.3, and the number of nearby devices was 3 with confidence 1.0, than the overall confidence of the conclusion of the first rule would be min(0.3,1.0)*0.6=0.18.
The same confidence would be calculated for the last rule, and both rules will be fired.
As a result, two ambiguous values of the attribute will be stored in the memory:
transportation_mode = car#0.18 transportation_mode = taxi#0.18
However, there is another table that produces values for transportation_mode attribute – the transportationModeB table.
This table sets the value of the transportation_mode attribute based on the analysis of mobile phone screen activity. If the user plays with the phone, it could mean that he or the is not driving a car.
Let us assume that only the last rule from this table is true.
According to disjunctive formula, the confidence of the transportation_mode set car will be min(0.3,1.0)*0.9=0.27
Now, we have following values in the working memory:
transportation_mode = car#0.18 transportation_mode = car#0.27 transportation_mode = taxi#0.18
transportationModeB was the last table that produces the value for transportation_mode (actually there is another one, but is is empty), hence the disambiguation process for these three values can begin.
This values are treated as cumulative values (i.e. they strengthen or weaken their confidence) and are evaluated according to cumulative formula from CF algebra presented in the last equation in the CF axioms section:
0.18+0.27-0.18*0.27=0.4014.
After running the example script given at the beginning of the section you should see the output presented below. Note, that the certainty factors of transportation mode is exactly the same as we calculated.
Attribute: daytype = workday cf = 1.0 Attribute: recent_activity = in_vehicle cf = 0.3 Attribute: vehicle_action = in_motion cf = 0.21599999 Attribute: past_activity = in_vehicle cf = 0.26999998 Attribute: notification = null cf = 1.0 Attribute: application_foreground = null cf = 1.0 Attribute: hour = 13.0 cf = 1.0 Attribute: transportation_mode = car cf = 0.40140003 Attribute: screen_active = false cf = 1.0 Attribute: payment = null cf = 1.0 Attribute: location = pay_zone cf = 1.0 Attribute: tariff = pay cf = 1.0 Attribute: day = tue/2 cf = 1.0 Attribute: bluetooth_count = 3.0 cf = 1.0
Set the value of the recent_activity to on_foot:
wm.setValueOf('recent_activity','on_foot')
Wait for a minute (literally, as this is what was set in the formula) and run the inference again twice (to force that the on_foot will appear more than 80% during last minute):
model.run(wm,inference=gdi,tables=['parkingReminder']) wm.showCurrentState()
You should now see that the vehicle_action changed from in_motion to start_parking and the value of the notification attribute was set appropriately to your time and day of a week. The sample output may look as follows:
Attribute: daytype = workday cf = 1.0 Attribute: recent_activity = on_foot cf = 1.0 Attribute: vehicle_action = start_parking cf = 0.24299997 Attribute: past_activity = in_vehicle cf = 0.26999998 Attribute: notification = start_parking_fee cf = 0.24299997 Attribute: application_foreground = null cf = 1.0 Attribute: hour = 13.0 cf = 1.0 Attribute: transportation_mode = car cf = 0.40140003 Attribute: screen_active = false cf = 1.0 Attribute: payment = null cf = 1.0 Attribute: location = pay_zone cf = 1.0 Attribute: tariff = pay cf = 1.0 Attribute: day = tue/2 cf = 1.0 Attribute: bluetooth_count = 3.0 cf = 1.0
Note, that the notification attribute was also set with lower certainty (the certainty equal to the minimal certainty of the conditional part times the confidence of the rule).
Certainty factors algebra axioms
Rule in CF algebra is represented according to formula:

Each of the elements of the formulae from equation~(\ref{eq:rule}) can have assigned a certainty factor
![Math $\mathit{cf}(element) \in [-1; 1]$](/lib/exe/fetch.php?media=wiki:latex:/img39dd59375278daad5482a28e6f296a84.png) where
where  means that the element is absolutely true;
means that the element is absolutely true;  denotes element about which nothing can be said with any degree of certainty;
denotes element about which nothing can be said with any degree of certainty;  denotes an element, which is absolutely false.
The CF of the conditional part of a rule is determined by the formulae:
denotes an element, which is absolutely false.
The CF of the conditional part of a rule is determined by the formulae:

The CF of conclusion  of a single \textit{i-th} rule is calculated according to a formula:
of a single \textit{i-th} rule is calculated according to a formula:
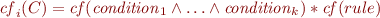
The 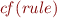 defines a certainty of a rule which is a measure of the extent, to which the rule is considered to be true. It is instantiated by the rule designer, or it comes from a machine learning algorithm (like for instance an association rule mining algorithms).
defines a certainty of a rule which is a measure of the extent, to which the rule is considered to be true. It is instantiated by the rule designer, or it comes from a machine learning algorithm (like for instance an association rule mining algorithms).
There are two types of rules: disjunctive and cumulative.
Disjunctive rules have the same conclusions but are conditionally dependent (i.e. value of any of the conditions determine values of other rules conditions).
The equation for calculating certainty factor of a disjunctive rule is presented in the following equation:

Cumulative rules have the same conclusions and have independent conditions (i.e. value of any of the conditions does not determine values of other rules conditions). The formula for calculating the certainty factor of the combination of two cumulative rules is given in the equation below.
Disjunctive rules
Disjunctive rules are the rules that have independent condition list.
The XTT2 convention suggest putting all of these rules within a single table.
The example of disjunctive rules are presented for example in table transportationModeA.
If there are several rules that produce the same conclusion (e.g. they set the value of transportation mode to car, only the most certain rules are selected for execution.
This applies to all different values that are set by the rules.
It means that in case of recent activity eq in_vehicle and bluetooth_count lte 4 are true, two last rules from the transportationModeA table will be executed, and the value of the transportation_mode attribute will be ambiguous, until all the tables that produce the value of transportation_mode are executed.
In case when there are only this two equally uncertain values in the memory, always the last value is chosen as the one that stays in the memory despite the conflict set resolution mechanism chosen for the inference.
Cumulative rules
Cumulative rules are rules that have the same attributes in decision parts and can be executed simultaneously in one reasoning cycle. The final conclusion is calculated according to the equation given in Certainty factors axioms section.
By XTT2 convention, the cumulative rules should be located in separate tables. However, if you choose fire all conflict resolution mechanism rules within a single table will also be treated as cumulative.
This mechanism is useful in strengthening or weakening conclusions that may depend on many different attributes, not related to each other.