Time-based operators

HMR+ language allows to parametrize the operators in rules' conditions with simple temporal quantifiers. This allows to refer to historical states in a statistical manner, giving additional tool for handling uncertainty (for more advanced tools for handling uncertainty refer to Managing uncertainty with Certainty Factors Algebra tutorial).

for the sake of this tutorial we will continue with the use case example given in HMR language quickstart and later extended in Callbacks and actions guide. If you did not read those tutorials, please go quickly through them.

More details on the time-based operators can be found in Bobek, S., Ślażyński M., Nalepa, G.(2015). Capturing Dynamics of Mobile Context-Aware Systems with Rules and Statistical Analysis of Historical Data. Paper presented at the Artificial Intelligence and Soft Computing.

In the example from the HMR language quickstart tutorial, the model set notifications depending on the parking zone, the user were in.

However, the system did not take into consideration the current activity of the user, so we did not know when the parking was started, or stopped, etc. We would like to implement the feature which would allow us notify the user about the necessity to pay parking fee only when the car was just parked, not all the time. In particular we would like to notify the user about the parking fee if the user got out of the car, i.e. his or her activity changed from in_vehicle to on_foot.

The informal definition of this fragment of the model could look as follows:

If the user past_activity was in_vehicle and
   recent user activity was on_foot 
then
   the user got out of the car (car parked)
   
If the user past_activity was on_foot and
   recent user activity was in_vehicle 
then
   the user got into the car (car started)
   
If the user past_activity was on_foot and
   recent user activity was on_foot 
then
   the car status stays unchanged (is parked)
   
If the user past_activity was in_vehicle and
   recent user activity was in_vehicle 
then
   the car status stays unchanged (is in motion)

The model presented below (partially) solves this problem by encoding the informal specification with time-based operators.

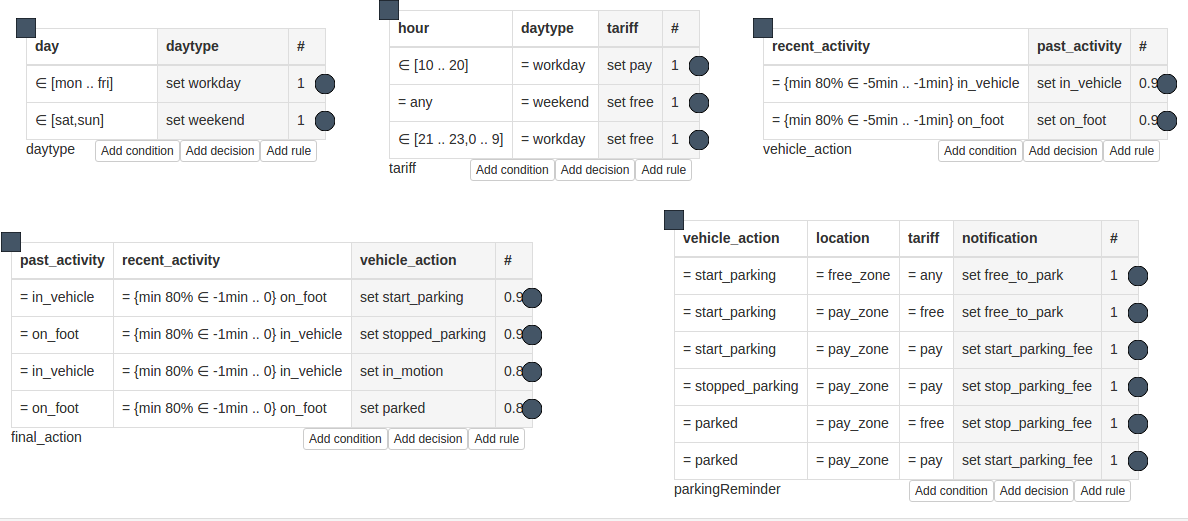
The complete model alongside with callbacks for hour and day attributes can be downloaded from here

To run the example, you will need the latest version of HaQuNa:

javac -cp haquna.jar:. *.java

Then, you can run a script that loads the model, sets the initial state and run the inference:

java -cp haquna.jar:. haquna.HaqunaMain --console test-script.hqn

You should see that the vehicle_action is set to in_motion as the script run the inference several times with value of recent_activity set to in_vehicle.

Set the value of the recent_activity to on_foot:

wm.setValueOf('recent_activity','on_foot')

Wait for a minute (literally, as this is what was set in the formula) and run the inference again twice (to force that the on_foot will appear more than 80% during lsst minute):

model.run(wm,inference=gdi,tables=['parkingReminder'])
wm.showCurrentState()

You should now see that the vehicle_action changed from in_motion to start_parking and the value of the notification attribute was set appropriately to your time and day of a week. The sample output may look as follows:

Attribute: notification  	= free_to_park  	 cf = 0.80999994
Attribute: daytype  	= weekend  	 cf = 1.0
Attribute: hour  	= 13.0  	 cf = 1.0
Attribute: recent_activity  	= on_foot  	 cf = 1.0
Attribute: vehicle_action  	= start_parking  	 cf = 0.80999994
Attribute: payment  	= null  	 cf = 1.0
Attribute: location  	= pay_zone  	 cf = 1.0
Attribute: tariff  	= free  	 cf = 1.0
Attribute: past_activity  	= in_vehicle  	 cf = 0.9
Attribute: day  	= sun/7  	 cf = 1.0

The numbers next to each of the attributes values marked as cf are certainty factors assigned to each values representing the confidence in the value. Some CF's are less than one, as we explicitly set that the confidence of the rules producing these values are lower (see last column of each table, with # in the header). For more on how to use certainty factors to handle uncertainty see Managing uncertainty with Certainty Factors Algebra tutorial.

Every logical operator (see HMR Language Grammar) in rules condition can be parametrized with time.

The example of the time-parametrized condition is presented below:

recent_activity eq {min 80% in -1min to 0} in_vehicle

It should be read as: if recent activity was equal for at least (quantitative relationship min) 80% (amount) of the time during (in) the last minute (-1min to 0), then …

More precisely, the elements of the parametrized operators are:

1. quantitative relationship – defining how is the amount of the states satisfying the condition related to the specified number of states. There are three possible relationships:
   • min (at least as many as . . . );
   • max (at most as many as . . . );
   • exact (exactly as many as . . . ).
2. amount – the second argument of the quantitative relation can be specified in two ways:
   • simply as a number (for example min 5 means “at least 5 states”);
   • as a fraction of the total number of states (for example exact 50% means “exactly the half of the states”).
3. vector of past states, which also can be written twofold:
   • as a range of non–positive numbers which should be regarded as indices of time samples relative to the current state designated by 0). For example -15 to 0 means last sixteen states including the current state.
   • using time units and Octave–like notation. For example -2h:1min:0 means last two hours of states sampled once per minute (121 samples including the current one).

Every time a reasoning is performed, the snapshot of a current state is saved to the HeaRTDroid memory. This is represented in Figure below by bold vertical lines labelled 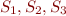. The inference can be invoked by many different causes like new sensor reading, expired attribute value, or on user demand. Therefore snapshots are taken in indeterministic time intervals.

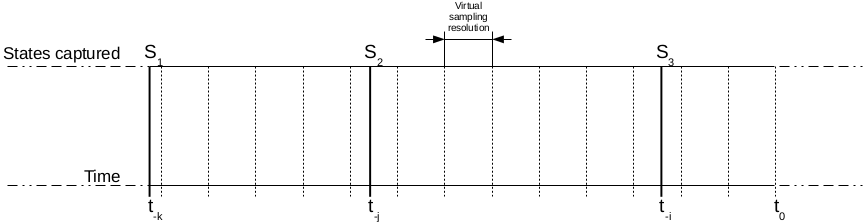
To allow statistical operations on attributes virtual sampling frequency is assumed – this is denotes as vertical dotted lines the Figure. Even though there is no actual snapshot at samples between and , all of the virtual samples will refer to last available state, in this case . Such approach allows for reliable statistical analysis of samples taken in variable intervals.